5a3f7ee4d82d
Question  Expand Transcribed Image Text We have seen that the Hilbert transform introduces a 90° phase shift in the compo- nents of a signal and the transfer function of a quadrature filter can be written as e H(f) = {0 f >0 f =0. We can generalize this concept to a new transform that introduces a phase shift of 0 in the frequency components of a signal, by introducing e-je f > 0 f = 0 eje Hạ(f) = {0 f < 0 and denoting the result of this transform by xa(1), i.e., X4(f) = X(f)H9(f), where Xe(f) denotes the Fourier transform of xe (t). Throughout this problem, assume that the signal x (t) does not contain any DC components. 1. Find hø (1), the impulse response of the filter representing this transform. 2. Show that xe(t) is a linear combination of x(t) and its Hilbert transform. 3. Show that if x(t) is an energy-type signal, xe(t) will also be an energy-type signal and its energy content will be equal to the energy content of x(t). Expert Answer谢谢亲的回惠顾,期待您的下次光临! 添加客服微信:bbwxnly,购买沟通交流so easy 欢迎咨询以下我们的一站式服务内容:课后习题解答查题|文件文档解锁下载|会员帐号包月月卡 Coursehero|Scribd|Studymode|Oneclass|Chegg|Studyblue|Termpaperwarehouse|SolutionInn|Bartleby|eNotes|Bookrags|SaveMyEaxms|Study.com|Studypool|Numerade |QuillBot|and more… 谢谢亲的支持,祝您学习愉快:) |
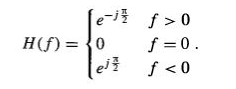
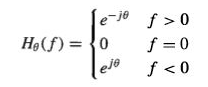
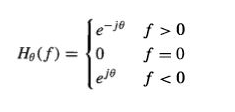 can be written as:
can be written as: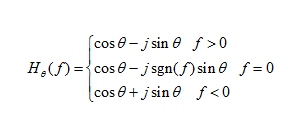
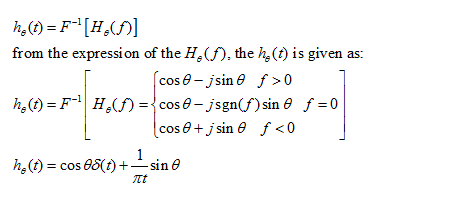
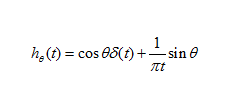
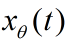 is the linear combination of the x(t) and its Hilbert transform.
is the linear combination of the x(t) and its Hilbert transform.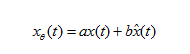
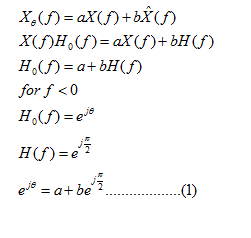
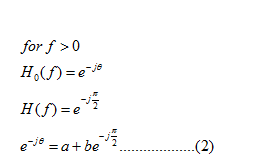
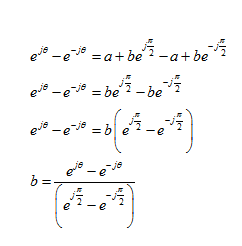
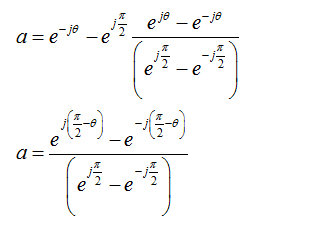
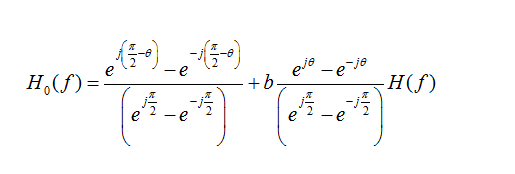
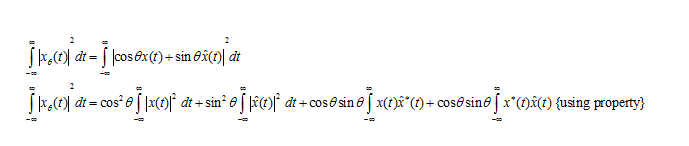
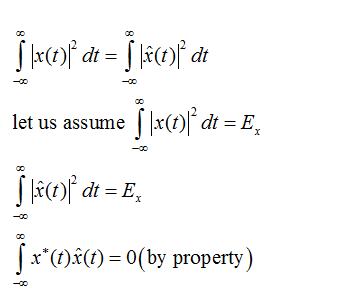
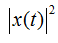 and the
and the 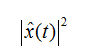 are the orthogonal signals. therefore the equation of the energy reduces to the form as shown below:
are the orthogonal signals. therefore the equation of the energy reduces to the form as shown below: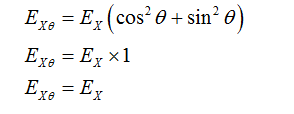
评论
发表评论